Decomposition and Problem-Solving
Everyone knows it’s easier to solve a complex problem if you break it up into simpler subproblems. This is called decomposition and it works in many domains. For example:
- A method I use when trying to answer a non-trivial question – and I don’t remember whence I got this – is to recursively break it down into subquestions until these start feeling answerable, and researching the subquestions, writing down more subquestions as they come up, researching those questions, et cetera. In the end I am left with a set of answers (my conclusions) and unanswered questions (my remaining areas of uncertainty).
- Back in January, describing How I Make Dungeon Synth, I mentioned decomposition’s usefulness in musical composition: “Musical form is recursive: larger forms are often constructed by combining smaller forms. They are boxes that contain other boxes that in turn contain further boxes. More atomic forms are simple phrases, brief musical passages that make some kind of sense on their own. Phrases are themselves made up of motives, which are even smaller units. I find that this is a useful framing, because problems are more easily solved when decomposed into smaller subproblems, and that is what this allows us to do with the problem of musical form.”
- When I program, I sometimes sketch a complicated procedure by making two to four calls (and no more) to other, yet to be written procedures. I continue recursively mapping out procedures until all of them are either compositions of other procedures or so simple that they are straightforward to implement.
- This is also how back-of-the-envelope calculations (and other Fermi estimations), cost-effectiveness evaluations and Multi-Attribute Utility Theory analyses work. See for example my rough estimate of how many cattle have died because of GMO scepticism in the EU.
As a rule, it’s easier to solve a series of simple subproblems than it is to solve one big complex problem directly. The argument:
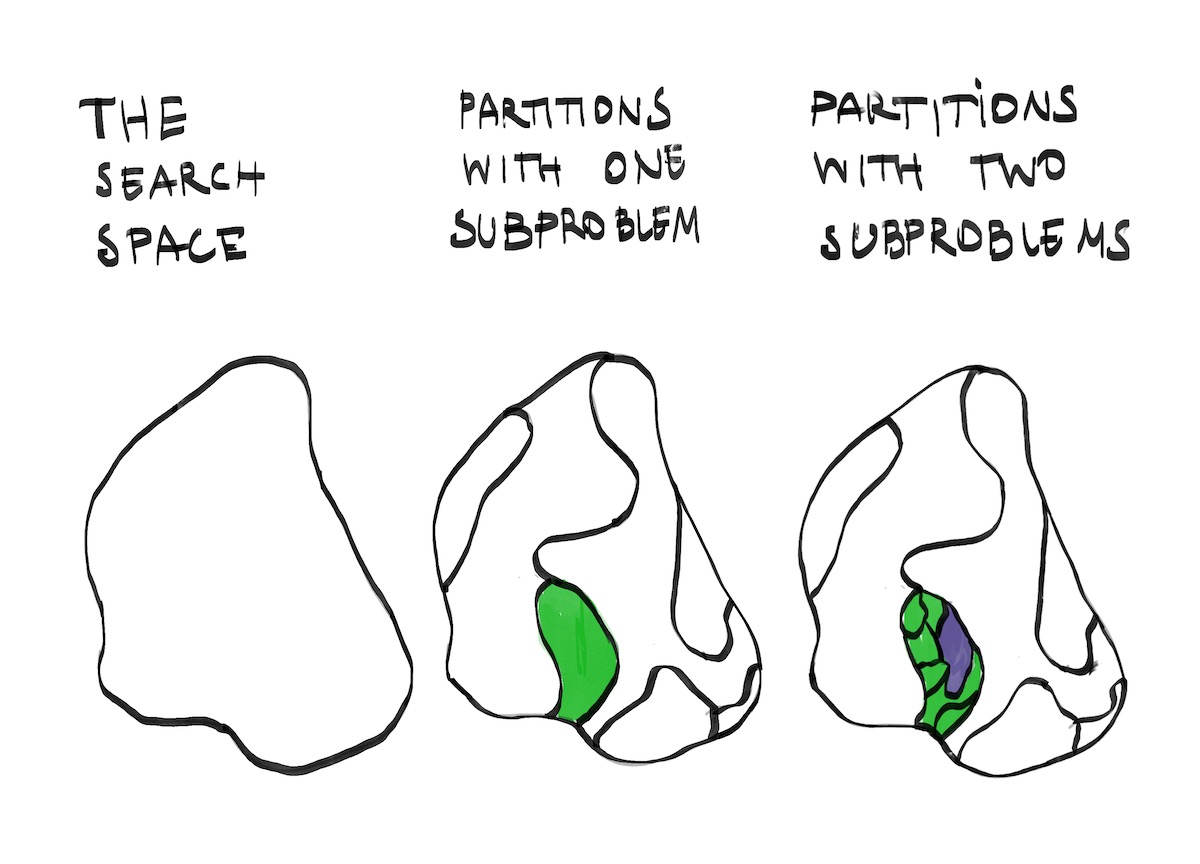
- Any problem has a set of possible solutions and non-solutions – this is the search space. When trying to solve a problem, we are searching this space for promising solutions.
- The size of a problem’s search space is the product of the sizes of the subproblems’ search spaces.
- Therefore, decomposing the problem will result in a non-linear reduction in size of the spaces we search in.
I know that sounds abstruse, so here is an example, a basic decision-making problem. Say I am trying to pick a restaurant for the anniversary dinner of my wife and myself. Suppose there are 7,000 restaurants in Berlin. That’s a pretty large search space. But I can split the problem into three subproblems:
- In which district do we want to eat?
- Which style of cuisine do we want to eat?
- Given a district and a cuisine, at which restaurant do we want to eat?
Berlin has 12 districts, and let’s say I divide all restaurants into 20 types of cuisine. That leaves an average of 7,000 ÷ 12 ÷ 20 = 29 restaurants for each combination of cuisine and district. Now, instead of trying to solve a problem with 7,000 possible answers, I solve first one with 12 possibilities, then one with 20 possibilities and finally one with (on average) 29 possibilities. That’s much more manageable. We could even look through all 29 possibilities to see which one we like more.
(Of course we usually only do something like this – we rarely make an exhaustive search, or split up problems consciously and deliberately – but the idea should be essentially the same; the difference is one of degree, and the difficulty of and time needed for any search are generally more substantial when the size of the search space is larger, and vice versa.)
These are some ways in which decomposition can lead to suboptimal answers:
- The search space gained by composing the subproblems is a subset or superset of the original problem’s search space. For example, maybe I was never going to consider any restaurant outside the district in which I live, in which case subproblem (1) was useless, or maybe I should consider restaurants outside Berlin, in which case subproblem (1) doesn’t capture the whole search space.
- The subproblem slices up the search space in very unequal parts. This just means the answer to the subproblem is obvious but does not help me make any progress on the original problem. (The most extreme example of this is a brute-force search.) For example, maybe I could have asked myself, “Do we want to eat at a theme restaurant?” and, having answered in the negative, that way ruled out a mere handful of possibilities.
- The subproblem slices up the search space based on average value, whereas I can actually expect to find the highest-value possibility in any partition. For example, maybe our ideal restaurant is in a place where there are few good restaurants, or serves a type of cuisine that is not among our favourites; in that case, choosing the district or cuisine with the best average restaurant means we would miss our top choice.
That means: Each subproblem should separate the search space into exhaustive, mutually exclusive and balanced parts.
Problem decomposition may be an example of the representational change theory of insight (Knoblich et al. 1999). The representational change theory says that we can make progress on a problem by viewing it differently. Decomposing a problem is one way of viewing it differently.[1] We can get stuck in a search space, and decomposition allows us to move to a fresh space, where we are not anchored to any particular area.
References #
Footnotes #
Another way brought up in Knoblich et al. (1999) is constraint relaxation. That means something like “thinking outside the box”. In my restaurant example, it might have entailed considering restaurants outside Berlin, or considering eating in, etc. ↩︎
