Quick Summaries of Two Papers on Kant and Game Theory
It’s not obvious from a Darwinian point of view why people (even people who aren’t related) often cooperate with one another. Researchers like Axelrod and Hamilton (1981) have used game theory to show that some strategies are both adaptive and favour cooperation. Though these projects may not say anything about how we should act towards one another[1], they do say something about why we do act the way we act. That’s important because we’d like moral strategies (under whatever view we think is more plausible) to outcompete immoral strategies; if we notice that various game-theoretic situations tend to steer people away from sound ethics, that’s both (1) an indication that these situations are to be avoided and (2) an invitation to think up situations that steer people towards better, more ethical strategies.
The rest of this post comprises summaries of two papers about this problem (specifically concerning my preferred ethics, Kantianism), plus some brief comments on each of them.
Laslier (2020): In the stag hunt game, two hunters choose to either hunt a stag or hunt hares – if both hunt the stag, they both get a very good payoff (the stag); if both hunt hares, they both get a bad payoff (few hares); but if one hunts the stag and the other hunts hares, the stag hunter gets a very bad payoff (nothing) and the hare hunter gets a good payoff (many hares). This game has two pure strategy Nash equilibria: the Pareto optimal outcome where both hunters hunt the stag, and the outcome where both hunters hunt hare. It also has one mixed strategy Nash equilibrium: both players hunt the stag with 2/3rds probability and hares with 1/3rd probability.
A “Kantian” player asks: “Which strategy is best if both players use it?”; the answer is to always hunt the stag. In a simple model, like that in Roemer (2019), a “Nasher” is a player that goes for one of the (non-Kantian) Nash equilibria. If a Nasher goes with the mixed strategy, they’re outcompeted by the Kantian. If a Nasher always hunts hares, they outcompete the Kantian if fewer than 2/3rds of the population are Kantians, and are outcompeted otherwise.
In a dynamic model, a “selfish” player optimises their own evolutionary fitness (by changing their strategy as they see fit). Without Kantians, the dynamic model reaches an equilibrium of hare hunting if a certain proportion of the initial population are hare hunters, and of stag hunting otherwise. With Kantians, either the selfish players outcompete the Kantians, or they reach an equilibrium with both Kantians and selfish players, again depending on the initial populations, as seen in these plots (where the selfish players adapt their strategy quickly on the left, and slowly on the right):
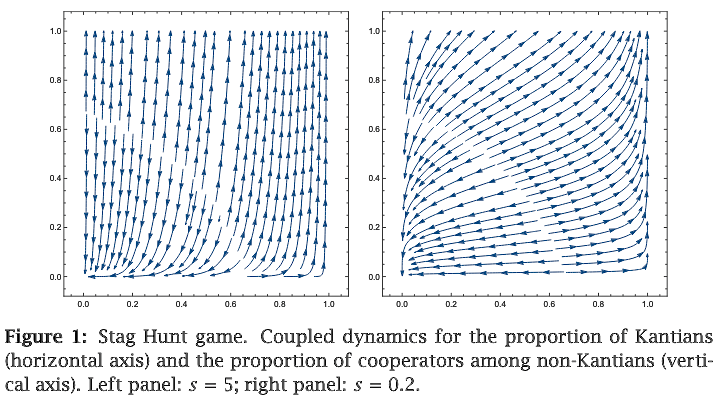
My commentary: “Kantian” is a stretch term here: in deontology, an action can’t be justified based on its consequences. (The next paper makes this difference clear.)
I feel like this paper says more about historical narratives like Game B than Kantianism: Game B holds that a civilisation that has solved collective action problems will outcompete civilisations that haven’t, but if we take this model to describe civilisations, it seems to suggest that a cooperative civilisation will have difficulty “bootstrapping” – it needs other cooperative civilisations for its strategy to work out; possibly a Game B civilisation needs to cooperate internally while competing externally. This also applies to groups and individuals within civilisations: even if they cooperate internally, they must compete externally. (But note that an important assumption in the stag hunt game is that agents don’t communicate, which of course is often not true in the real world.)
Maybe an insight here is something like “deontology, which privileges cooperation, looks better from a consequentialist point of view the more deontologists there are” or maybe more nicely expressed in the form of a maxim: A lone deontologist is a bad consequentialist, but a society of deontologists are good consequentialists. And also: When playing stag hunt, having a critical mass of deontologists makes cooperation a winning strategy for selfish players too. All this assuming that Kantians and other deontologists really would cooperate every time, which brings us to the next paper.
White (2009): In the prisoner’s dilemma game, two (let’s say innocent) criminals either confess (betraying one another) or stay silent – if both confess they both get long sentences; if both stay silent they both get short sentences; but if one confesses and the other stays silent, the confessor gets a very short sentence and the silent one gets a very long sentence. The game’s only Nash equilibrium is where both criminals confess, an outcome which is dominated by the one where both stay silent. That is, agents acting out of rational self-interest will always confess, even though both staying silent produces a better outcome for them than if they both confess.
A naïve Kantian might (like a “Kantian” player in the previous paper) always choose to cooperate (“do the action that’s best when everyone does it”), so it might seem that naïve-Kantianism solves the prisoner’s dilemma. The actually-Kantian categorical imperative (as represented by the Formula of Universal Law) comes in two flavours: (1) act according to a maxim that, if practiced universally, doesn’t thwart the intended action and (2) act according to a maxim that, if practiced universally, doesn’t undermine our ability to rationally decide what’s good or our freedom to pursue the good. Neither (1) nor (2) seems to prohibit confessing; (2) implies a duty to help others, but it’s an imperfect duty (roughly, one that’s not mandatory). The actually-Kantian categorical imperative (as represented by the Formula of Humanity) says that we shouldn’t treat people as mere means, but always also as ends; this also does not seem to prohibit confessing. So it seems that for the actually-Kantian staying silent in the prisoner’s dilemma is good but not required (again, assuming the criminals are innocent).
My commentary: This paper nicely outlines the difference between “consequentialist” universalisation and Kantian universalisation. The fact that the former produces reliably better outcomes in the prisoner’s dilemma isn’t much evidence against Kantianism, since Kantianism doesn’t accept judging right and wrong by outcomes. That’s assuming that consequentialist universalisation is taken to imply “do the action that’s best for everyone when everyone does it” and not “do the action that’s best for me when everyone does it”. The first interpretation is even further from Kantianism than the second, since it involves aggregating utilities.
References #
Footnotes #
On the one hand, it’s weird to justify an ethics by saying it’s evolutionarily adaptive. On the other hand, it’s even weirder to advocate an ethics that’s totally alien to human nature. On the third hand, we’re really not supposed to derive oughts from ises. On the fourth, from where are we supposed to derive oughts? ↩︎
